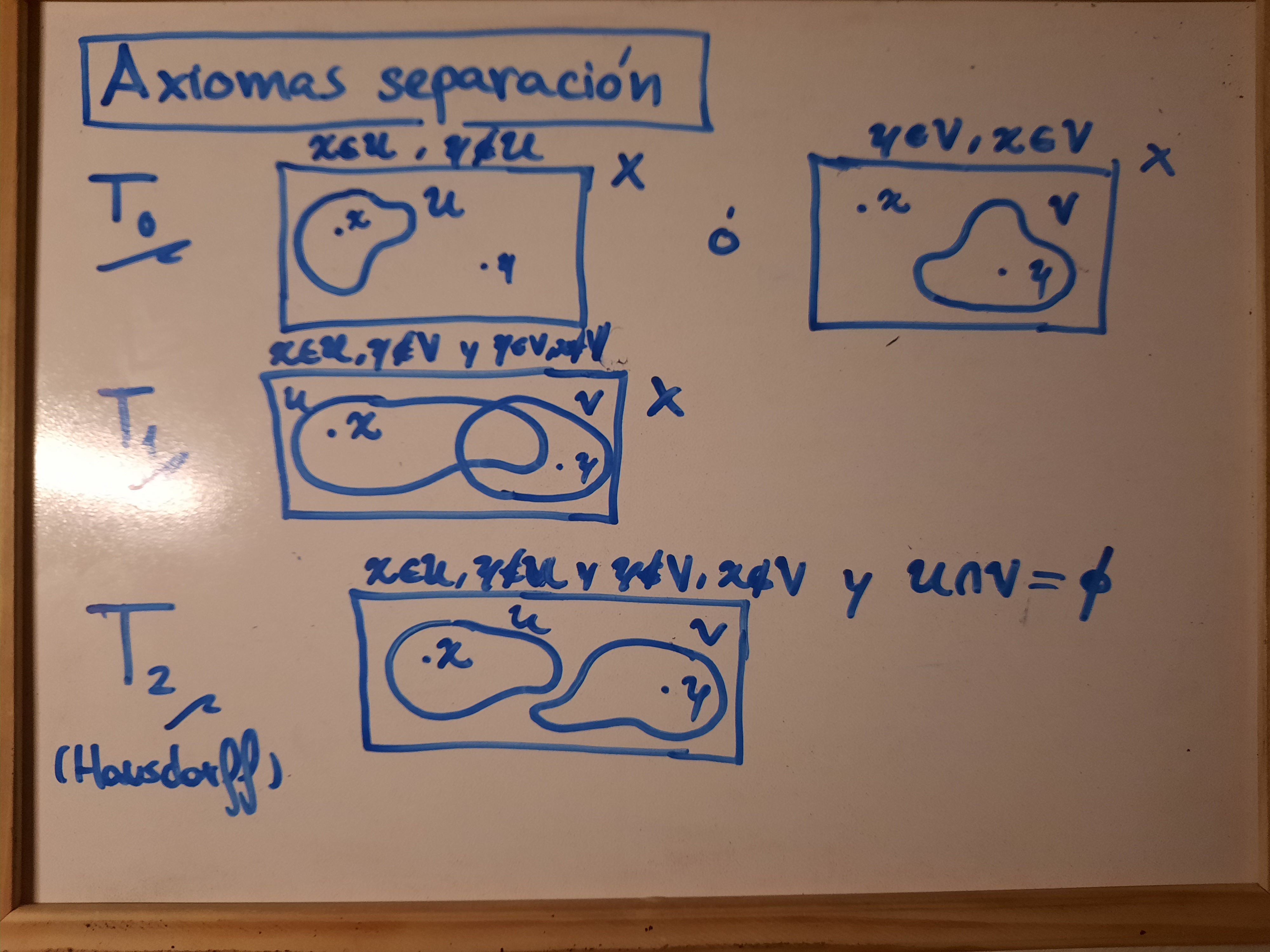
Axiomas de separación

Axioma de separación $T_{0}$

Un espacio topológico $(X, T)$ se dice que es $T_{0}$ si para todo par de puntos distintos $x, y \in X$ , o bien existe un entorno $U$ de $x$ con $y \notin U$ , o bien existe un entorno $V$ de $y$ con $x \notin V$ .

Axioma de separación $T_{1}$

Un espacio topológico $(X, T)$ se dice que es $T_{1}$ si para todo par de puntos distintos $x, y \in X$ , existen un entorno $U$ de $x$ con $y \notin U$ y un entorno $V$ de $y$ con $x \notin V$ .

Axioma de separación $T_{2}$

Un espacio topológico $(X, T)$ se dice que es $T_{2}$ (o un espacio de Hausdorff) si para todo par de puntos distintos $x, y \in X$ , existen entornos $U$ y $V$ de $x$ e $y$ , respectivamente, tales que $U \cap V = \emptyset$ .

Relación entre los axiomas de separación

$T_{2} ⟹ T_{1} ⟹ T_{0}$

Ejemplos

Todo espacio metrizable es Hausdorff.
Cualquier conjunto simplemente ordenado con la topología del orden es Hausdorff.

Propiedades

Los tres axiomas de separación son hereditarios (los subconjuntos también los tienen).
Los tres axiomas de separación son invariantes topológicos.

$Axiomas de Separación.jpg|400$

Axioma de separación T0

Axioma de separación T1

Axioma de separación T2

Axioma de separación $T_{0}$

Axioma de separación $T_{1}$

Axioma de separación $T_{2}$